-
생존분석 (SPSS)SPSS 2019. 11. 17. 19:54lung.sav0.00MBsmoking.sav0.00MB
생존분석은 의학연구에서 굉장히 흔히 쓰이는 분석기법이지만, 꽤 흔한 빈도로 잘 못 사용되는 분석법 이기도 하다. 언뜻 생존분석은 로지스틱 회귀분석과 비슷하다는 생각이 들 수도 있지만, 생존분석에는 시간이라는 개념이 들어가기 때문에, 시간에 따른 변화를 읽어내지 못한 채 분석을 하게 되면 잘못된 결과를 얻을 수 있다.
거기에다 SPSS의 생존분석에는 이러한 오류를 찾아내고 교정할 수 있는 방법이 결여되어 있어 특히 더 주의를 요한다. 개인적인 생각으로는 생존분석을 시행하는데 SPSS를 쓰지 않는게 좋겠다고 말하고 싶지만 여러 이유로 SPSS를 제외하고는 선택지가 없는 경우도 있기 때문에 무조건 강요하기도 힘든 것이 사실이다. 이에 이번 포스트에서는 생존분석의 실질적인 측면에 대해 살펴보기로 하자.
1. Kaplan-Meier curve
상당수의 의학논문에서 생존분석을 이용해서 분석을 하는 경우, Kaplan-Meier curve를 제시하고 그 후 cox 분석을 주요분석법으로 사용한다. Kaplan curve를 보여주는 이유는 아무래도 단조로운 논문에 그래도 그림이 하나쯤은 필요하기 때문이기도 하지만 더 큰 이유는 cox 분석을 사용하기 위한 주요 가정 중 하나인 proportional hazard assumption을 만족하는지를 Kaplan curve가 rough하게 보여주기 때문이다. 비례위험가정은 생존분석의 가장 중요한 가정이기 때문에 뒤에서 따로 다룰 예정이다. 우선 Kaplan curve에 중심을 두고 진행해 보자.
우선 생존분석을 다루기 위해서는 시간을 다루는 것에 익숙해져야 한다. 대개 질병과 사망을 다루는 경우, 연구대상자는 일정 시점(time 1)에 특정 질환이 진단되어 연구대상자에 포함되게 된다. 그 후 일정 시간이 흐른 후(time 2) 연구대상자는 사망하거나(event) 다른 이유로 연구대상에서 빠지게 된다(censoring).

A~D까지 4명의 연구대상자 가 있다고 가정해보자. 대상자 A는 2002년(time1)에 연구에 진입한 후 2008년(time2) 사망(event)하였다. 대상자 B는 2001년(time1) 진단 후 2005년(time2) 연구대상에서 loss (censoring)되었다. 대상자 C는 2002년(time1) 진단 후 2010년(time2) 연구 종료 때까지 생존(censoring)하였다. 이를 SPSS에 입력할 때, SPSS에서는 time을 하나만 입력할 수 있기 때문에 time1을 0으로 맞춰놓을 수밖에 없다(대개 status는 censoring을 0, 사망을 1로 입력하는 것이 일반적이다.).
만약 진단시점(time1)을 0으로 고정하게 되면,

분석 > 생존분석 > Kaplan-Meier


대부분의 생존분석은 위와 같이 진단시점 (혹은 초기시점)을 0으로 고정한 후 분석을 진행하기 때문에 시간을 하나만 입력할 수 있다는 점이 큰 문제가 되지는 않지만, 경우에 따라 time1과 time2를 모두 입력해서 분석하도록 강요받는 상황도 존재한다.
자 그럼 smoking.sav 에 있는 데이터를 이용해서 본격적으로 그림을 그려보자.
분석 > 생존분석 > Kaplan-Meier

금연 후 실패에 관한 데이터이다. 금연 연구에 왠 생존분석? 이라고 생각할 수도 있지만 금연 후 실패를 사망으로 간주한다면 생존분석으로 분석 못 할 이유는 없다. 그런 경우 생존분석(survival analysis)라는 용어대신 event history analysis라는 용어를 쓰기도 하지만 의학연구에서는 상관없이 생존분석 용어를 사용하는 경우가 더 많다.
상위급 저널에서는 Kaplan curve를 제시하면서 아래와 같이 No. at risk를 제시하기를 원하는 경우도 있다 이런 경우

이런 경우 중위값은

위의 표 우측에 보이는 중위수의 추정값이 되며,
No. at risk는 생존표에서의

해당 그룹에서의 남아있는 케이스 수가 된다. 예를 들어 시간 grp 0에서 시간이 0 일때의 No. at risk는 63이 된다 (시간 0이 시작할 때의 남아있는 케이스 수).

만약 시간 50에서의 No. at risk는 시간 49에서 event가 있은 후 56까지는 없기 때문에, 49에서의 24명이 되게 된다.
마지막으로 proportional hazard에 대한 언급을 해 보자. cox 분석은 여러 분석법 중 신경 쓸 일 많지 않은 쉬운 분석법 중에 하나이다. 하지만 비례위험 가정은 꼭!!! 어기면 안 된다. 비례위험 가정에 대해 예를 들어보면, 암환자의 경우 진단 후 초/중반에는 사망위험이 높지만 시간이 지날수록 사망 위험도는 점차 감소하다, 5년 이상 생존하는 경우 사망위험이 일반인보다 약간 높을 정도까지 낮아진다. 만약 새로운 항암제의 효과에 대해 연구하고 싶다면 신/구 항암제의 위험도 차이가 초반에나 후반에나 동일해야 한다는 것이다.
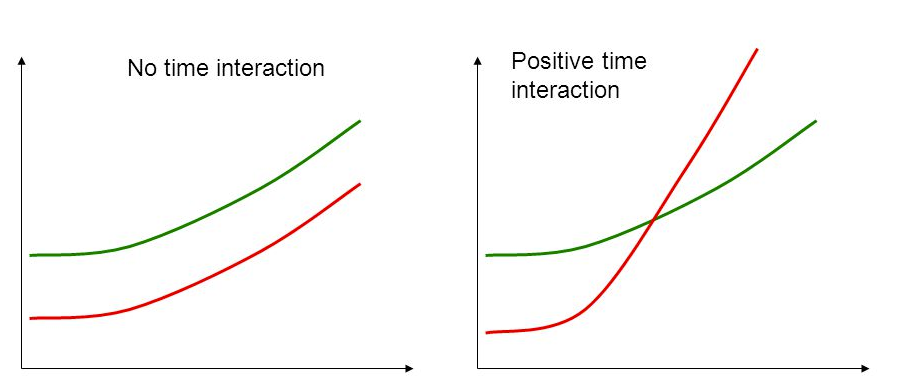
왼쪽 그림과 같이 시간에 상관없이 위험도는 동일한 간격을 가져야 한다. 만약 오른쪽 그림과 같이 위험도가 일정한 간격을 지니지 않을 경우 시간에 대해 별도의 배려를 해야만 한다.
분석 > 생존분석 > Kaplan-Meier

비례위험가정을 확인하는 법은 몇 가지 방법이 있지만 SPSS에서 가능한 방법은 누적위험함수 그래프를 확인하는 법과 Cox 분석 내에서의 time dependent covariate를 압력하는 방법 2가지 이다. 결과가 통계적으로 유의하더라도 Kaplan curve 및 위험함수 그래프에서 두 선이 접점을 가지게 되면 비례위험가정을 만족하지 못하는 것으로 생각하는 편이 맞다(정확히는 Scheonfeld residual을 구해서 확인해야 하는데 SPSS에서는 이 과정이 불가능하다.). 그리고 논문 첫 figure로 Kaplan curve를 넣는 이유 중 하나가 비례위험가정만족을 보여주는 그림이기 때문이다. 만약 Kaplan curve에서 두 선의 교차가 발생했는데도 불구하고 시간에 대한 별도의 배려 없이 논문이 진행되었다면 독자들은 그 이후 결과를 전체적으로 신뢰할 수 없게 될 것이다. (상대적으로 Kaplan curve에서는 비례위험가정을 만족하더라도 대상자의 수가 적어지는 후반부에 교차(접점?)가 일어날 가능성이 있다. 다른 방법으로 비례위험가정을 확인했고 문제가 없다면 누적위험함수 그래프를 대신 제시하는 것도 하나의 방법이다.)
중간 정리를 해보면
1. 접점 유무를 보기 위해 Kaplan curve를 요구하는 것이다.
2. 만약 접점이 있는 경우에도 무시하고 일반적인 방법으로 분석하면... 결과는 무조건 reject 이다.
2. Cox 분석
Cox 분석의 정식 명칭은 proportional hazards model regression analysis이다. 정식 명칭을 보면 앞에서 왜 그토록 proportional hazard assumption을 강조했는지와, Cox 분석도 일반화선형회귀분석의 한 분류라는 것을 알 수 있다. 전체적인 분위기는 로지스틱회귀분석과 놀라울 정도로 닮아 있다. 잔차분석이 그리 중요하지 않다던가... 연속형 변수 사용에 유의해야 한다던가... 하여간 앞의 금연 데이터를 이용해서 Cox 분석을 맛봐보자.

데이터를 보면 대충 감이 오겠지만, 이 데이터는 금연치료에 패치만 쓴 그룹과 패치와 약물치료를 같이 한 그룹으로 나누어 금연치료의 효율성을 본 연구이다. 따라서 이 연구의 결과변수(Y)는 시간(ttr)과 재발여부(relapse)가 결합된 결과이며, 원인변수(X)는 치료그룹(grp)이 된다. 그 외 나이라던가 흡연년수...은 covariate로 보면 될 것이다.

시간의 분포를 보면 연구의 대략적인 결과를 파악할 수 있다. 생존분석에서 시간은 사망하거나(event), 연구에서 중도탈락(censoring)한 두 가지 경우 중 하나이다. 시간의 histogram을 보면 전체적으로 right shifted 된 느낌인 가운데 0과 200근처가 우뚝 서있는 것을 볼 수 있다. 0에 가까운 봉우리는 아마도 작심삼일 들일 것이며, 200에 가까운 봉우리는 연구 종료에 따른 censoring일 것이다. 위 그림을 보면 연구 종료를 제외하면 censoring이 없음을 알 수 있다. 이는 이 연구가 굉장히 잘 관리된 연구 결과임을 보여준다.
대부분의 연구에서 무시되고 있는 내용인데, 생존분석에서 중도탈락은 무작위(random)하게 이루어지는 것으로 가정된다. 하지만 실제 연구에서는 중도탈락이 의미를 지니는 경우가 많다. 치료약의 부작용이 심하거나, 환자가 스스로 판단하기에 호전이 없을 경우, 무작위 배정 결과가 중간에 환자에게 노출되어 위약군 환자가 연구에서 빠져나가는 경우... 어찌 보면 중도탈락은 사망결과만큼이나 중요한 결과이지만 일반적인 cox분석 결과에서는 중도탈락을 결과물로 제시하지 않는다. 하지만 연구 결과를 판단할 때 신약의 치료효과가 아무리 좋더라도 이해할 수 없는 이유로 치료군 혹은 placebo군의 중도탈락이 반대편에 비해 의미가 있을 정도로 많다면 그 결과는 신뢰하지 않는 것이 바람직하다.

본격적으로 Cox분석을 해보면,
분석 > 생존분석 > Cox 회귀




Cox분석 결과를 보면 피치만 사용한 경우 약과 같이 치료한 경우보다 금연에 실패할 가능성(상대위험도)이 1.83배(95% CI: 1.20~2.80)높다고 나온다(로지스틱회귀분석에서는 exp(β)가 오즈비가 되지만 생존분석에서는 상대위험도로 불린다.). 그리고 원하는 결과의 기준이 복합치료라면 exp(-β)값인 0.55를 계산하는 방법도 있고 아래와 같이 reference 값을 바꿔주면 원하는 결과를 얻을 수 있다.


3. Cox 분석에서 연속변수의 처리법
로지스틱회귀분석에서와 같이 생존분석에서도 연속변수를 분석하는 데에는 주의가 따른다. 따라서 적절한 값을 기준으로 잘라서 범주형 변수로 분석하는 것이 합리적이다. 하지만 대상자의 수가 많지 않아서 범주형 변수로 잘랐을 때 통계적으로 유의해지지 않는다던가, 범주형 변수로 변환하더라도 어느 값을 기준으로 몇 개의 범주로 나누는 것이 합리적인지 판단할 때에는 연속형 변수를 이용한 분석이 도움이 될 때도 있다. 이때 사용되는 것이 Martingale 잔차이지만 SPSS에서는 이를 지원하지 않기 때문에, SPSS를 이용해서 생존분석을 하는 경우 연속형 변수를 분석에 투입하면 안 된다.
변수를 범주화시킬 때 주의사항은 임상적인 의미를 가지는 절단점이 있는 경우 그 점을 우선시하되, 나눈 후 각 범주에 속한 대상자들이 어느 정도 균등해지는 것도 고려해야 한다. 만약 systolic BP를 기준으로 한다고 했을 때 가장 최적의 절단점은 140일 것이다. 하지만 어떤 이유로 140mmHg 이상 혹은 이하의 대상자가 아주 많거나 적으면 그 변수를 분석에 투입한다고 해도 의미를 잃을 것이다. 그렇다고 systoloc BP를 quantile 값으로 나눠서 넣으면 분석은 잘되겠지만, 논문의 심사자 혹은 독자들은 왜 이걸 이리 잘랐지?라는 의문을 가질 수밖에 없다. 따라서 케이스 바이 케이스의 적절한 판단이 요구될 수 밖에 없다.
4. Proportional hazard assumption
Kaplan curve 설명할 때 비례위험가정의 중요성에 대해서 이미 언급한 바 있다. 생존분석을 제대로 하느냐 못하느냐는 이 가정을 얼마나 이해하고 있느냐에 달려있을만큼 중요한 내용이다.
proportional hazard 가정을 확인하는 방법으로는
1) Kaplan curve 이용한 육안적 확인
2) Schenofeld residual 그래프 이용한 육안적 확인
3) Scheonfeld method 이용한 통계적 확인
4) time dependent covariate 투입 후 통계적 유의성 확인
4가지 방법이 있다. SPSS에서는 2와 3번 방법은 불가능하다. 하지만 생존분석에서 비례위험가정의 중요성을 감안하면 다른 방법이 존재하며 이 부분은 SPSS의 한계가 있음을 알아야 한다.
4-1) Kaplan curve 이용한 육안적 확인
비례위험가정을 확인하기 위해 lung.sav파일을 열어 확인해보자.




폐암환자의 성별에 따른 Kaplan curve와 위험함수 그래프이다. 앞에서 언급했듯이 논문에 Kaplan curve를 넣는 이유는 비례위험가정을 만족하는지 확인하기 위함이라고 하였다. Cox 분석에서 통계적으로 유의성을 가지는 변수가 (유의성 없는 변수는 접점이 몇 개 있던 몇 번 교차하던 상관없다.) Kaplan curve에서 접점을 지니거나 교차하면 비례위험 가정에서 벗어나 있을 가능성을 고려해야 한다.
다만 실제 논문에는 위의 예제와 같이 성별에 따른 Kaplan curve보다는 논문의 주 목표인 치료법에 의한 Kaplan curve를 주로 넣게 될 것 같다. 문제는 시간이 어느 정도 흘러서 양쪽 그룹에 대상자가 줄어들게 되면 Kaplna curve에서는 비례위험 가정을 만족하는 상태에서도 접점 비슷한 모양이 보일 수 있다는 점이다. 당장 위의 예제만 봐도 시간 800근처에서 접점이 생길 뻔했다.
비례위험가정의 확인은 어디까지나 위험함수를 가지고 하는 것이다. 편의 상 Kaplan curve를 논문에 넣기는 하지만 위의 예와 같이 누적위험함수에서는 별 문제없어 보이지만 Kaplan curve에서는 접점 비슷한 것이 보이는 경우, Kaplan curve를 그림으로 넣은 상황에서는 논문 내에 비례위험 가정이 어쩌고저쩌고 말로 변명해봐야 소용없는 경우가 있을 수 있다. 따라서 이런 경우 약간 덜 일반적일지라도 차라리 위험함수곡선을 제시하거나 아니면 SPSS말고 다른 통계 패키지를 이용해서 Schenfeld 잔차를 구해 이를 제시하고 그림은 Cox curve를 제시하는 것도 하나의 방법이다.
하여간 Kaplan curve건 위험 함수 그래프이건 접점을 가지는 것은 비례위험가정을 만족하지 않는다는 것을 보여주는 상황이며 이에 대해서는 적절한 대응이 필요하다.
Kaplan curve로 비례위험가정을 확인하는 방법의 문제점은 1) 정확하지 않다. 점점이 없다고 비례위험가정을 만족하는 것도 아니고, 접점이 있다고 만족하지 않는 것도 아니다. 2) 연속형변수에 대해서는 대응할 수 없다. 계속 나오지만 SPSS를 이용한 생존분석에서는 연속형변수 쓰면 안 된다.
4-2 & 4-3) Scheonfeld method


SPSS를 제외한 다른 통계패키지에서는 Scheonfeld 잔차를 구해서 비례위험 가정을 확인 할 수 있다. 위의 그림은 연속형변수 형태의 의사가 측정한 Karnofsky score (ph.karno변수)의 비례위험 가정을 확인한 것이다. 위의 그림은 초기에는 karnofsky score가 낮은 위험도와 연관되어 있지만 시간이 흐른 뒤에는 유의해지지 않는 모습을 보여주고 있으며, 아래 붉은 색의 박스내의 p-value는 결론적으로 비례위험가정을 만족하지 못함을 보여주고 있다. 다른 통계패키지의 결과라서 눈에 안들어오는게 당연함에도 이 결과를 보여주는 이유는 되는것과 안되는 것을 구별할 줄 알아야 하기 때문이다. 비례위험 가정에 관해 문제가 생기면 차라리 통계자문을 구하는 것이 더 바람직하다.
4-4) time dependent covariate 투입 후 통계적 유의성 확인
마지막 진단방법은 time dependent covariate를 투입한 후 통계적 유의성을 확인하는 방법이다. 이는 진단과 함께 치료법이 되기도 하지만... 모든 변수에 대해 이걸 다 시도해 본다는 것은... 솔직히 권유하고 싶지 않다. 따라서 이 방법은 Kaplan curve에서 비례위험가정이 무너졌음을 확인했을 때 주요변수에 한해 시도해 볼 수 있을것 같다.
만약 시간의 변화에 따라 hazard가 변화한다면 time*covariate의 상호작용은 통계적으로 유의할 것이다. 우선 이 방법의 긍정적인 측면은 비례위험가정의 진단 및 치료라는 점이다.
분석 > 생존분석 > 시간종속 Cox 회귀창을 열게 되면 계산창이 눈에 들어오게 된다. 여기서 time*covariate를 정의해 준다.

왼쪽 창의 맨 위 Time(T_) 항목이 시간 항목이다. 아래 time변수와는 다르니 주의하자!
여기에 우리가 보려 하는 ph.karno변수를 곱해주고 오른쪽 위의 모형 버튼을 눌러주면,

왼쪽 맨 위의 T_COV_ 항목이 우리가 계산한 Time(T_)*ph.karno 항목이다.
이 둘을 넣은 후 Cox 분석을 하면

ph.karno 변수와 time*ph.karno 변수 둘 다 통계적으로 유의함을 알 수 있다. 이로써 ph.karno변수는 비례위험가정에 어긋남을 확인할 수 있으며, 또한 이게 비례위험가정을 벗어난 ph.karno변수에 대한 대처법이 되기도 한다.
이리 쉽게 끝나면 좋은데... 통상적으로
1) time*covariate
2) log(time)*covariate
3) rank(time)*covariate
비례위험가정을 벗어난 변수에 대해서는 최소한 이 세가지 형태에 대해서는 시도해보는 것이 정석이다. 문제는 Schenfeld 잔차 그래프의 지원을 받지 못한 상황에서 순전히 감에 의존해서 이를 진행하기에는 무리가 있는것도 사실이다. 하여간 SPSS로는 한계가 있으니 하다가 잘 안되면 남에게 맡기자.
5. non-proportional hazard의 교정
비례위험 가정이 깨진 경우 이를 해결하기 위한 방법은
1) 연구기간을 줄일 수 있는지 확인한다.
2) stratification이용
3) time dependent covariate 투입
의 3가지 방법이 현실적이다.
1) 연구기간 확인
아무래도 연구기간이 길어지면 비례위험가정이 깨지는 경우가 흔하다. 당장 위의 폐암 예를 봐도 진단 당시 Karnofsky score는 초기 300일 까지 정도까지만 유효하다. 이때 만약 연구기간을 300일 까지로 변경한다면 비례위험가정은 만족되는 상태가 된다. 특히 암환자 연구에서 5년 생존을 보게 되면 변수 중 몇 개 이상은 비례위험 가정에 어긋나는 경우가 흔하다. 필요 없이 긴 추적관찰 기간이 연구에 오히려 해가 되는 경우가 있을 수 있다. 아래 2가지 방법이 어려운 경우 연구기간을 줄이는 방법이 가장 현실적이다.
2) Stratification

만약 비례위험가정을 벗어난 변수가 주요변수가 아니라면 stratification을 시행하는 것이 가장 좋은 방법이다. 성별을 아래 계층칸에 넣은 후 분석하면, 아주 쉽게 해결된다. 다만 논문의 method 항목에 변수 **는 proportional hazard assumption을 만족하지 못해서 stratification method를 사용하였음.. 이라고 언급해 주어야 하며 stratification을 시행한 변수에 대해서는 결과가 출력되지 않는다.
3) time dependent covariate 투입
위에 언급했으니 다시 언급하지는 않겠다.
6. Stanford Heart Transplant Data
비례위험가정 이외에도 생존분석에 주의할 부분이 있다. 아래 그림은 이전에 연구되었던 심장이식 연구의 관찰연구자료이다.

심장이식 그룹의 생존이 훨씬 나은 것을 알 수 있다. 실제로 이대로 이 결과는 저명 학술지에 발표되었고, RCT까지 진행한 후에 효과가 없음이 밝혀졌다. 이는 심장이식 순서를 기다릴 수 있을 정도로 건강한 사람만이 심장이식군으로 포함되었기 때문이다 (심장이식 기다리다 죽은 사람은 control group). 심장수술을 기다리는 기간을 따로 분리하면 다음과 같아진다.

이러한 상황은 관찰연구에서 굉장히 흔한 상황이며, 아직까지도 수많은 연구에서 동일한 오류가 반복되고 있다. 비록 이 포스트에서는 이런 자료를 어떻게 처리할지 다루지 않겠지만, 관찰연구에서는 치료까지의 대기시간의 유무가 연구결과에 영향을 끼칠 수 있음을 알고 있어야 한다.
7. Cox 그래프
대개의 경우 논문에 넣을 그림으로 Kaplan curve를 사용하지만 Cox curve를 넣는 경우도 종종 보인다. 앞에서도 언급했다시피 Kaplan curve는 비례위험가정 만족 여부를 확인시켜주기 때문에 흔히 사용되지만, expert 들이 big journal에 싣는 경우 비례위험가정 확인이 그다지 필요 없기 때문에 결과를 더 잘 보여주는 Cox graph를 선호하기도 한다.

8. 마무리하며
생존분석은 상대적으로 신경 쓸 부분이 적기는 하지만 비례위험가정 만족 여부와 관찰 연구의 경우 치료까지의 대기시간 같은 결과에 영향을 미칠 수 있는 부분은 신중하게 접근해야 한다. 그 외에는 로지스틱회귀분석과 비슷한 방법으로 접근하면 큰 문제는 없을 것이다.
'SPSS' 카테고리의 다른 글
복합표본자료분석 - 2. 자료준비 (SPSS) (0) 2019.11.19 로지스틱회귀분석 (SPSS) (0) 2019.09.10 다변수분석법 (SPSS) (0) 2019.09.07 탐색적 자료분석 3-3. 세 변수의 상호작용 (SPSS) (0) 2019.08.29 탐색적 자료분석 3-2. 두 변수의 관계 파악 - 연속 변수 vs 범주형 변수 (SPSS) (0) 2019.08.28