-
로지스틱회귀분석 (SPSS)SPSS 2019. 9. 10. 12:47
분석 > 회귀분석 > 이분형 로지스틱이전까지는 주로 선형회귀분석방법에 대해 알아보았다. 선형회귀분석법은 다른 분석방법을 배우기 위한 기본과정이기 때문에 많은 시간을 할애해서 배울 필요성이 있기는 하지만, 실제로 논문작성에서 그리 많이 사용되는 방법은 아니다. 하지만 이번에 다룰 로지스틱회귀분석법은 극단적으로 말하자면 관찰연구의 대부분을 차지하는 방법이다. 아마 대부분의 임상의사는 로지스틱회귀분석+생존분석으로 평생 욹어 먹을 가능성이 크다. 그런 만큼 세심히 알아보자.
1. 로지스틱회귀분석의 기본원리
원래 학문적 배경이 수학이나 통계 쪽이 아니라서 숫자 나오면 두통이 발생하기 시작한다. 하지만 그래도 이해를 위해 어쩔 수 없이 알아야 하는 과정이 존재한다. 머리 덜 아프게 그리스식 알파벳은 사용 않고 최대한 쉽게 설명해 보려 한다.
로지스틱 회귀분석은 확률을 다루는 분석법이다. 나이가 증가함에 따라 당뇨 확률이 어떻게 변하는가? 허리둘레와 당뇨 확률의 관계는 어떤가?... 등등... yes/no를 비율을 다루는 분석법이다.
확률을 다룸에 있어서,
1) 대개 yes는 1, no는 0 으로 처리한다.
2) 그렇게 되면 어느 시점에서의 확률은 평균치와 동일해진다. (BMI 30인 사람 10명 중 당뇨환자가 5명이었다면 당뇨 확률은 (0*5+1*5)/2=0.5, 즉 50%이다.)
3) 확률은 최소치가 0이며, 최대치는 1이다. (0~1 사이 범위를 벗어날 수 없다.)
4) 3)에 의해 확률은 선형일 수 없다. (왜냐하면 BMI와 당뇨 확률이 선형이라면, BMI가 아주 낮은 경우 당뇨확률은 -가 되어야 한다. 마찬가지로 BMI가 아주 높은 경우 당뇨확률은 1을 넘어야 한다.--> 그런 수치가 나오는 BMI가 현실성이 있느냐 없느냐와는 다른 얘기다. 선형관계인 경우 무조건 확률이 0~1 범위를 벗어날 수 있다는 것 자체가 중요하다.)
이런 문제를 해결하기 위해 사용된 방법 중 하나가 로지스틱 곡선이다.
로지스틱회귀분석에 사용되는 표준로지스틱 함수는,
$$y=\frac{e^x}{1+e^x}$$
이다. 그래프로 그려보면,

위와 같은 그래프가 그려진다. x가 -∞ 이어도 y는 0 미만으로 내려가지 않으며, x가 ∞여도 y는 1을 넘지 않는다. 흔히 말하는 시그모이드 형태의 대표적인 곡선이다. 하지만 이런 형태의 곡선이 여럿 존재하는데 로지스틱 곡선이 최강자가 된 이유는 계산이 쉽기 때문이다.
$$odd=\frac{p}{1-p}$$
$$log(odd)=logit=log(\frac{p}{1-p})$$
$$log(\frac{y}{1-y})=x$$

아주 심플해졌다. 로지스틱회귀분석이 많이 사용되는 이유는, 확률이 로지스틱 곡선을 만족한다고 가정하면, 확률의 로그오즈값(로짓값)을 선형회귀방정식으로 구할 수 있다는 것이다.
한 단계 더 진행해 보자.
첨부파일인 DM.sav 파일을 연 후 HbA1c 수치에 따른 당뇨 진단 확률의 그래프를 살펴보자.
그래프 > 레거시 대화상자 > 선형차트 > 단순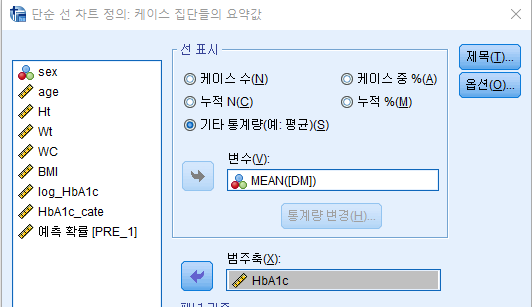

대략적으로 HbA1c 수치가 증가하면 당뇨로 진단될 확률이 증가됨을 알 수 있지만, 그래프 후반부로 가면 위아래로 진폭(흔들림)이 커짐을 알 수 있다. 이는 오른쪽으로 갈수록 대상이 되는 샘플의 수가 작아져서 확률을 제대로 반영하지 못 해서 생긴 일이다. 이러한 형태는 변수를 로그변환을 이용해서 정규화 함과 함께 HbA1c수치를 좀 더 단순화(그룹화?) 함으로써 해결할 수 있다.

변환 > 변수계산

변수 계산의 TRUNC 명령어는 소수점 아래를 버리는 명령어이다. 위 예제와 같이 10을 곱한 후 소수점 아래를 버리고 다시 10을 나눠주게 되면 소수점 아래 첫자리까지만 남기게 된다. 그 결과 그래프가 좀 더 단순해 짐을 볼 수 있다.
이 확률 그래프를 위의 표준 로지스틱 함수의 그래프와 비교하면,
처음 확률은 둘 다 0에서부터 시작하지만, 당뇨 확률 그래프의 후반부는 1이 아니다.
라는 것을 알 수 있다.
그럼 과연 이 확률을 로지스틱 회귀분석에서는 어떻게 인식하고 있을지 살펴보자.
분석 > 회귀분석 > 이분형 로지스틱
그래프 > 레거시 대화상자 > 선형차트 > 단순

로지스틱 회귀분석이 어떤 방식으로 진행되는지 대충 감이 잡히는지?
그런데... 이 결과를 좋다고 받아들이기에는 2가지 문제가 있다.
1) HbA1c와 로그 오즈(당뇨)의 관계는 진짜로 선형인가? 선형회귀분석때는 그래프 그려서 선형 확인했었는데... 확률은 그래프 그리기 만만치 않다. 아마 선형 아닐 거다. 자연적인 관계에서 완전 선형은 그리 쉽지 않다.
2) 확률의 천장이 진짜 1 맞는가? 바닥은 0 맞아 보이는데, 천장은 내 눈에는 1보다 낮은 수치로 보인다.
이 문제를 해결하기 위한 방법은,
1) 웬만하면 로지스틱 회귀분석에서 독립변수로 연속 변수는 사용하지 않는다. 전부 범주형 변수로 바꿔 사용하면 선형성 문제를 벗어날 수 있다. 아니면 일반 가법 모형(Generalized Additive Model) 쓰는 방법도 있기는 한데.... 아마 의학계열에서는 리뷰어 심사 통과하기 힘들 거다(틀렸다는 얘기는 아니다. 그 분야에서 흔히 쓰이지 않는 분석법을 이용하면 리뷰어에게 받아들여질 가능성은 0으로 수렴한다. 그럼에도 불구하고 꼭 필요하다면 우선 진행한 후 이 논문 저 논문에 받아들여질 때까지 계속 투고하는 방법밖에는 없다.).


위의 결과는 HbA1c를 번주화 시킨 후 분석한 로지스틱 회귀분석 결과이다. 변수를 범주화시키면 로지스틱 회귀분석에서 생길 수 있는 많은 문제가 동시에 해결된다. 다만 연속 범주를 몇 개의 범주로 나눌지에 대한 고민이 필요하다.
2) 연구대상 설정 단계부터 주의한다. 다른 말로 하면 당뇨 진단 유무에 대해 연구하고 싶으면 연구 대상자가 당뇨의 유병률이 어느 정도 이상 되는 집단이 되도록 설정하라는 얘기다. 나이를 중년 이후로 한정한다던가... 위의 예제는 HbA1c 6.5 이상이면 다른 거 필요 없이 당뇨이다. 따라서 후반부 확률은 1에 가까울 것이 예측되는 상황이었다. 그런데도 실제로 보니 후반부도 1보다 낮아 보인다. 로지스틱 회귀분석은 확률을 무조건 0~1 사이에 분포시킨다. 이번 분석은 천장이 1에 가까우니 문제없지만 만약 천장이 0.5보다 낮으면... 사실 이런 문제 신경 안 써도 큰 문제는 없다. 하지만 n 수 끌어 모으려고 아토피 연구에 80대 노인까지 넣는다던가... 흡연 연구에 초등학생까지 집어넣는 일은 하지 말자. n 수 늘리려다 오히려 연구가 망가지는 경우가 있다.
2. 결과변수(Y) 설정
그럼 이제 본 분석으로 넘어가 보자. 분석법으로 로지스틱 회귀분석을 사용하는 경우는 1) 처음부터 결과변수가 이 분형 변수일 때와, 2) 결과변수가 연속 변수나 그 비슷한 형태이었는데 필요에 의해 이분형 변수로 나눈 경우 두 가지 경우가 있다. 첨부파일 중 DEP.sav 데이터를 열어보자.
dep데이터는 65세 이상 노인의 우울증 점수(PHQ-9)를 보기 위한 가상의 데이터이다.
연구의 목적(study question)이 "과연 직업 여부는 독거노인의 우울증 점수에 영향을 미치는가?"라고 한다면 원인 변수(X)는 직업 유무가 될 것이며, 결과변수(Y)는 우울증 점수가 될 것이다(두 명의 주인공). 그 외 다른 변수들은 보정변수(들러리)로 처리하면 된다. 당연한 얘기겠지만 주인공에게는 좀 더 따뜻한 관심을 가져야 한다. 직업 유무는 occu 변수(1:있음, 0:없음)이며, 우울증 점수는 PHQ변수이다. 직업 유무는 이분형 변수이니 우선은 넘어가고 PHQ-9에 대해 먼저 살펴보자.


다시 자료로 돌아와서 PHQ-9 점수의 분포를 살펴보면,
분석 > 기술통계량 > 데이터 탐색

전형적인 right-shift 되어있는 자료이다. 우선 예로 내려오는 말에 따라 로그 변환(0이 포함되어 있으니 정확히는 log(PHQ+1))해보면,

좀 even 하게 펼쳐지긴 했지만 아직도 right-shift 되어 있는 상태이다. 더욱이 이 문제는 0점이 대부분이어서 생긴 문제이기 때문에 변수 변환을 한다고 해결되지 않는다. 변수 변환 후 연속 변수로 처리하는 것은 문제가 있으니 다음 단계는,
1) 최솟값 그리고 최빈값이 0이며, 정수로 된 값이니 0-inflated poisson이나 0-inflated negative binomial 분포를 가정하고 분석하는 법 (SPSS에서는 불가능한 방법이다.)
2) 설문 해석 법대로 none, mild, moderate, moderately severe, severe로 분리해서 순서형 로지스틱 분석(ordered logistic regression) 시행
3) 두 단계로 나눠 로지스틱 회귀분석 시행
이 될 것이다.
자료는 단순하게 만들수록 안에 담긴 정보를 잃는다. 따라서 정보의 질은 1>2>3의 순서로 볼 수 있다. 근데 문제는 1번과 2번 방법은 분석도 어렵고 해석은 더 어렵다는 점이다. 개인적으로는 분석 및 해석이 용이한 로지스틱 회귀분석을 이용해서 진행하고, 만약 n수가 적어서... 등의 이유로 더 많은 정보가 필요하다면(통계적으로 유의한 결과를 얻는데 실패한다면) 그때 다른 방법을 고려해 볼 수 있을 것이다.
자 그럼 로지스틱 회귀분석으로 결정 났으니, 어딘가를 절단점으로 잘라야 한다. 절단점을 결정함에 있어서 고려할 사항은 1) 임상적 판단과 2) 통계적 판단이다.
1) 임상적 판단: 절단점은 임상적으로 의미를 지녀야 한다. 다른 말로 하면 절단한 이유가 합당해야 한다. 이분형 변수를 최대한 효율적으로 분석하기 위해서는 절단점이 중심값(median)인 경우가 가장 좋다. PHQ-9의 median은 2점인데, 2점은 임상적으로 아무 의미가 없다(PHQ-9 interpretation table 참조). 0/1 기준으로 자르면 우울증 유무로 나눌 수 있고, 9/10 기준으로 자르면 상담 및 약물치료가 필요한 우울증으로 나눌 수 있다. 임상적 의미를 가진다는 말은 이런 의미이다.
2) 통계적 판단: 절단한 후의 대상자 수는 50/50이 되는 것이 가장 이상적이다. 흔히 연구 대상자 수를 언급할 때 무조건 n수가 많으면 좋은 것으로 착각하는 경향이 있다. 때문에 아토피 연구에 노인을 포함하는 만행을 저지르는 것이다. 대상자가 만약 10만 명이라도 연구 대상자의 결과변수 분포가 99999/1 명이라면 이건 유의할 수 없는 연구이다.
연구 대상자가 얼마나 돼야 하나의 명확한 정의는 존재하지 않지만, 아무리 관찰연구라도 100명은 넘기는 것이 좋다. 예전에 차트 찾아 논문 낼 때는 50명만 넘으면 어떻게 해 보려 했었는데... 그래도 SCI급 논문을 노린다면 100명이 안되면 좀... 많을수록 좋기는 한데 최소 100은 넘기게 해 보자. 그다음은 실질적인 연구대상자이다. 결과변수 분포가 98/2명이면 실질적 대상자는 4명(2+2)이다. 물론 진짜 대상자 수가 4명인 연구에 비하면 +alpha가 존재하지만 4명으로 이해하는 것이 좋다(이해 안 가고 납득할 수도 없으면 effect size에 대해 찾아볼 것). 대상자가 50/50이어야 비로소 100명짜리 연구가 되는 것이다.
결과변수 분포의 경험적인 하한 값은 30%이다. 위에서 천장이 어딘지 본 기억이 나는가? 로지스틱 회귀는 확률이 무조건 0과 1 사이에 분포한다고 가정한 후 진행한다. 따라서 확률이 낮을 때는 0에 가까워야 하며, 높을 때는 1에 가까워야 한다. 경험적으로 결과변수의 분포 하한 값이 30%가 안된다면 천장이 1에 비해 결과에 영향을 줄 정도로 많이 낮을 가능성이 있다. 그 부분을 염두에 두고 진행해야 한다.
이런 두 가지 측면을 고려한다면 절단점으로 고려 가능한 부분은 0/1, 4/5, 9/10 셋 중 하나가 될 것이다.

만약 절단점을 0/1로 한다면 대상자의 분포는 41.46/58.54, 실질적 대상자수는 1190명(595*2)이 될 것이다. 절단점이 4/5인 경우는 대상자의 분포는 77.07/22.93, 실질적 대상자수는 658명(329*2), 9/10인 경우 대상자의 분포는 90.73/9.27, 실질적 대상자수는 266명(133*2)이다. 순수 통계적인 측면에서는 절단점 0/1이 가장 좋은데, 임상적인 의미를 고려한다면 4/5도 그리 나쁘지 않다(PHQ-9를 해석하는 방법에 따라 0~4를 하나로 묶기도 한다.). 임상적인 의미는 9/10이 가장 좋지만 9/10의 경우 실질적 대상자가 상당히 많이 줄어들게 된다. 9/10이 꼭 필요하다면 대상자를 더욱 늘리는 방법 (혹은 아예 우울증 환자 집단과 같은 우울증 유병률이 높은 집단을 대상으로 연구 대상 자체를 바꾸는 방법)을 생각해 봐야 한다. 이런저런 측면을 고려해서 이번 예제에서는 4/5를 절단점으로 하기로 했다(어디까지나 이건 내 주관적인 판단이다. 임상적 의미와 통계적 의미의 판단은 연구자 스스로 판단하는 것이 좋다.).
3. 탐색적 자료 분석
다음 단계는 탐색적 자료 분석이다. 로지스틱 회귀분석에서 탐색적 자료 분석은 아무래도 선형 회귀분석 때에 비해 제한적이다. 우선 개별 변수의 분석은 선형 회귀 때와 같으니 생략하고 두 변수의 분석을 살펴보자.
분석 > 기술통계량 > 교차분석



로지스틱 회귀분석은 결과변수(Y)가 이분형 변수이기 때문에 독립변수가 연속 변수인 경우 t-test, 범주형 변수인 경우 카이 스퀘어검정을 사용해서 table 1을 작성하게 된다. t-test는 이전에 다뤘으니 넘어가고 카이스퀘어 검정은 위와 같이 하면 된다. 가끔 보면 X가 순서를 가진 범주형 변수인 경우 p for trend 결과를 대신 제시하기도 하는데, 이건 X를 연속형 변수로 처리하겠다는 의미이다. 만약 X를 연속형 변수로 처리할 마음이 없다면 p for trend는 필요 없는 사족이다.
단변 수분석은 다음과 같다.
분석 > 회귀분석 > 이분형 로지스틱
로지스틱 회귀분석에서 범주형 변수의 처리는 우선 모든 변수(연속형과 범주형)를 모두 변수항에 투입한 후 위의 그림 우측 위의 범주형 변수 항목에서 따로 지정해 주는 방식을 이용한다. 그리고 이전 포스트를 봤으면 알겠지만 로지스틱 회귀분석은 일반화 선형 모형 항목에서도 가능하다. 다만 결과 도출법이 약간 달라서 결과가 약간 다를 수는 있다. 그리고 옵션 항목에서 exp(B)에 대한 신뢰구간 항목을 체크해야 90% 신뢰구간이 계산된다.


카이 스퀘어 검정 결과와 마찬가지로 단변수 분석에서도 occu 변수에 따른 depression은 유의하다. 위에서도 언급했듯이 로지스틱 회귀분석상의 estimate는 log odds 값이기 때문에 exponential 값이 우리가 원하는 오즈비 값이다. 위 내용을 해석해보면 직업이 없을 경우 우울증이 있을 오즈비는 1.401(95% CI: 1.067-1.840)이다. 혹은 직업이 있을 경우 우울할 가능성이 29% 낮다 (1/1.401=0.714). 그리고 범주형 항목에서는 참조 범주 (reference category)를 처음 값 혹은 마지막 값(SPSS 기본 설정 - 일반화 선형 모형에서는 초기 설정이 처음 값으로 되어 있음)으로 설정 가능하다. 참조 범주에 따라 해석이 반대이며 특히 독립변수가 이분형 변수인 경우 결과에는 보이지 않는다. 해석에 주의할 것!!!
다음은 age 변수이다.

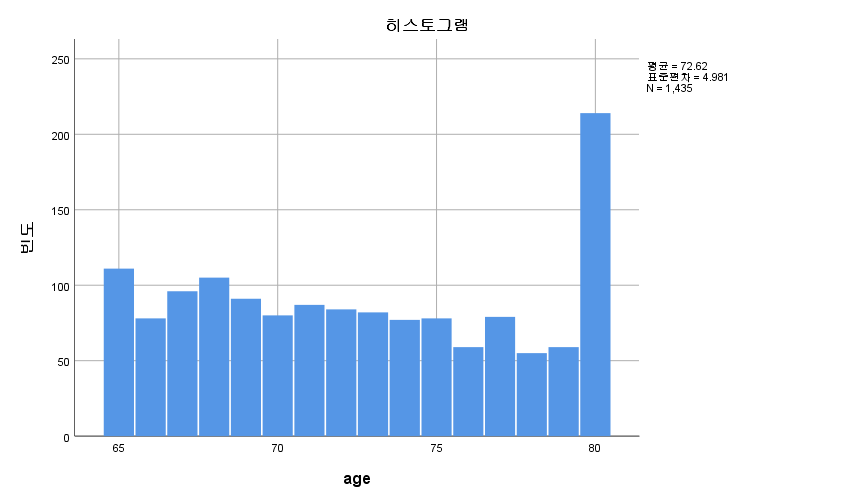
연속 변수 형태인데 어째 65세와 80세만 많다. 히스토그램 분포상으로는 left-shift? even? 하게 분포되어있기는 한데... 한 수치만 많은 경우 이걸 정규화시킬 필요는 없다. 나머지 수치들은 고르게 분포하고 있는데 수치 하나를 바로잡겠다고 정규화시키려다가 오히려 더 망가지기 때문이다. 거기에 age변수는 주인공인 X나 Y가 아니라 엑스트라이다. 큰 문제없으면... 거기에 주 분석법이 로지스틱 회귀 분석이므로, 연속형 변수는 웬만하면 범주화하는 게 맞다. 그래서 5씩 끊어서 age_cate 변수를 만들었다.

연속 변수를 끊어서 범주형 변수를 만드는 법은 위와 같이 변수 계산을 이용하는 법과 코딩 변경 명령을 사용하는 법 2가지 방법이 있다. 우선 같은 변수로 코딩 변경 명령어는 사용하지 않는 게 좋다. 왜냐하면 변경 전 항목 위에 덮어쓰는 방식이기 때문에 실수했을 때 되돌릴 방법이 없다. 남은 것은 변수 계산을 이용한 방법과 다른 변수로 코딩 변경 명령어가 있는데 각각 장단점이 존재한다. 다른 변수로 코딩 변경은 동일한 간격이 아니라도 원하는 지점을 절단점으로 원하는 항목만큼 자를 수 있다는 장점이 있으나 부등호 문제 및 범위지정을 잘못할 경우 변환이 안되고 빠지는 변수들이 존재하게 된다. 때문에 변환 후 항상 결측이 존재하는지 확인할 필요가 있다. 이에 비해 변수 계산은 동일한 간격으로 자르는데 편하며 변환이 안 되는 변수가 없다는 장점이 있지만 원하는 지점을 지정해서 절단할 수 없다는 단점 또한 존재한다.

나이는 유의하지 않다.
독거 여부의 경우를 보면,

독거 상태인 경우 (solo=1) 유의하게 우울증일 확률이 증가한다. 위험도가 1.391배 높다 or 39.1% 높다.(원래는 오즈비로 표현하는 게 맞는 표현이다. 그런데 유병률이 낮은 경우 오즈비는 상대위험도와 비슷해지며, 해석도 상대위험도와 비슷하게 한다. 논문 표현에서도 계속 오즈비 어쩌고 하는 것보다 통상 위험도가 얼마 높고 낮다는 표현이 통상적으로 사용된다. 하지만 어디까지나 로지스틱 회귀분석의 결과는 오즈비이다.)
사족으로, 인과관계의 해석에는 주의해야 한다. 지금 이 분석 결과는 단면 연구이기 때문에 인과관계를 포함하고 있지 않다. 우울하기 때문에 독거 상태가 된 건지, 독거 상태라서 우울한 건지 알 수 없다는 얘기다. 다이아몬드 예제에서도 보았듯이 이런 식으로 영향력이 있는 변수는 다른 변수의 결과를 일 그러 뜨릴 수 있다. 다변수 분석 및 상호작용을 잘 살펴봐야 한다.
월수입을 보면, (변환 > 시각적 구간화 명령을 이용해서 동일한 대상자를 가지도록 5 등분했다.)

월수입이 연구 대상 중 상위 20%인 범주(기준 범주)에 비해 월수입이 낮아질수록 우울증이 있을 오즈비가 증가하게 된다. 상위 20%에 비해서 21~40%는 우울증을 가질 오즈비가 0.971(95% CI:0.623-1.513)으로 유의한 차이를 보이지 않았지만, 상위 41~60%는 오즈비가 1.748배, 61~80%는 1.695배, 81~100%는 2.339배 였으며 통계적으로 유의했다.
4. 다변수 분석

다변수 분석 상 성별과 월수입만 유의했고, 그 외 이번 연구의 목표인 직업 유무는 유의하지 않았다.
로지스틱 회귀분석에서는 다변수 분석 후에 잔차 검정의 중요성이 크지 않다. 아무래도 결과변수가 0/1로 한정되어 있어서 하나의 관측치가 전체적인 모형을 뒤틀 위험성이 크지 않아 그런 것으로 보인다. 잔차 검정은 넘어가더라도 독립변수 중 연속 변수가 존재하는 경우 다중공선성에 대해서는 한 번 확인하고 넘어가는 것이 좋겠다. 다중 공선성은 선형 회귀분석 항목에서 측정 가능하며 다중공선성은 결과변수와는 상관없으니 아무 변수나 넣고 돌려도 결과는 동일하다.
여태까지 로지스틱 회귀분석에 대해 알아보았다. 로지스틱 회귀분석은 일반적으로 잔차 검정 및 이상치 검사의 필요성이 그리 크지 않아 초보자들도 무리 없이 분석 가능하다고 알려져 있지만, 그래도 신경 써야 할 부분이 존재하는 것도 사실이다. 이런 부분을 신경 써 준다면 좋은 결과를 얻을 수 있을 것이다.
Take Home Message
1. 결과변수의 비율을 신경 쓰자.
2. 연속 변수는 되도록 범주화시켜서 분석
'SPSS' 카테고리의 다른 글
복합표본자료분석 - 2. 자료준비 (SPSS) (0) 2019.11.19 생존분석 (SPSS) (0) 2019.11.17 다변수분석법 (SPSS) (0) 2019.09.07 탐색적 자료분석 3-3. 세 변수의 상호작용 (SPSS) (0) 2019.08.29 탐색적 자료분석 3-2. 두 변수의 관계 파악 - 연속 변수 vs 범주형 변수 (SPSS) (0) 2019.08.28