-
탐색적 자료분석 3-1. 두 변수의 관계 파악 - 연속변수 vs 연속변수 (R)R 2019. 8. 5. 14:32
이전 포스트에서 탐색적 자료 분석의 첫 단계로 연속형 변수에 대한 정규성 검증 및 정규 변환을 하는 법에 대해 알아보았다. 그 외에 자료 안에 결측치가 몇 개나 존재하는지? 최대치와 최소치가 어느 정도이며 최소-최댓값의 범위가 상식적인 범위 내인지 확인이 필요하다. 탐색적 자료 분석 과정 자체가 원래 귀찮은 노가다의 연속이지만 쓸만한 결과를 얻기 위해 꼭 필요한 과정이기도 하다. 이전 포스트의 첨부자료인 normal.Rdata 파일을 이용해서 분석을 계속해보자.
library(car) library(psych) library(dplyr) library(ggplot2)1. 개별 변수의 확인 (이전 포스트 재탕)
이전 포스트에서 연속변수의 정규성 확인 및 정규 변환을 하면서 개별 변수의 확인 부분을 얼추 다루었다. 그 부분을 다시 확인하면,

summary 명령어를 이용해서 자료의 구조를 확인할 수 있다. 연속변수의 경우 최대/최솟값뿐 아니라 평균과 중간값도 알 수 있다. 카테고리 변수의 경우 몇 개의 팩터로 구성되었는지, 그리고 분포는 어떻게 되는지 알 수 있다. 뿐만 아니라 summary 명령을 이용하면 결측치를 확인할 수 있다. 결측치가 있는 경우

위의 pred1항목과 같이 아래 부분에 NA (Not Assigned, 결측치)의 개수를 확인할 수 있는 것을 볼 수 있다.
그다음 단계로 psych library의 describe 명령을 이용해서 carat과 price 두 연속변수의 형태를 확인해 보자.
hist(diamond$carat) describe(diamond$carat)

hist(diamond$price) describe(diamond$price)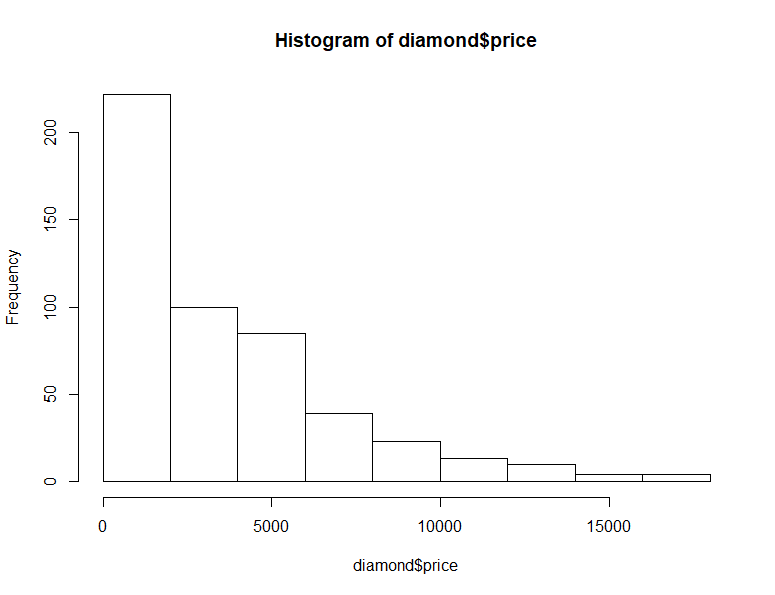

히스토그램 상 전형적인 정규분포의 형태 (종모양) 까지는 아니더라도 최소한 평평하게? 골고루? 분포해야 하며 skewness와 kurtosis 두 항목이 ±2 이내이면 일단 넘어갈 수 있다고 했다. 하지만 위의 carat과 price 변수 둘 다 히스토그램부터 Right-shifted되어 있어서 로그 변환 후에야 좋아짐을 확인했었다.
2. carat과 price 두 변수의 관계 확인
두 연속 변수의 관계를 확인하는 가장 좋은 첫 단계는 그림을 이용해서 확인하는 것이다.
with(diamond, plot(carat,price))
변환 없이 두 변수의 dotplot을 보면 위와 같은 모습을 보이고 있다. carat이 증가함에 따라 price도 증가? 비싸지지만 왠지 깨끗한 직선 형태는 아닌 것 같다. 그리고 점들의 밀도도 carat과 price 가 0에 가까운 부분은 밀도가 높지만 비싸고 큰 다이아들이 존재하는 부분은 밀도가 작다. 사실 이런 모습들을 해소하기 위해서 이전 포스트에서 두 변수에 대해 로그 변환을 시행한 것이다. 우선 그래프 모양만 로그 형태로 바꿔보자.
with(diamond, plot(carat,price, log="xy"))
다음은 로그 변환한 변수들의 그래프이다. (위는 축의 변환, 아래는 변수의 변환 비슷해 보이지만 다르다.)
with(diamond, plot(log(carat),log(price)))
로그 변환하니 두 변수의 관계가 직선에 가깝다. 이런 경우 감사히 여기고 선형 회귀분석을 시행하면 된다. (사실 변환 후 이렇게 예쁘게 되는 경우는 극히 드물다. 대부분의 경우는 이보다 훨씬 지저분한 관계를 보여준다.)
3. carat과 price 두 변수를 이용해서 선형회귀분석
다음 단계로 상관관계를 볼 수도 있겠지만, 어차피 상관관계가 논문 table에 들어가는 내용도 아니고 하니 곧장 단변수 선형 회귀분석을 시행하려고 한다. 성격 급한 분들이 하는 실수 중 하나가 변수들과의 관계를 충분히 고려하지 않은 채 곧장 다변수 분석으로 들어가는 것이다. 이런 경우 실수도 많아지지만 변수간 상호작용 같은 꼭 필요한 부분까지 무시하게 된다. 나중에 다시 언급하겠지만 1) 개별 변수의 분석 (x, y), 2) 두 변수의 관계 파악(y와 x의 관계), 3) 3변수의 상호작용 파악 (y와 x1, x2의 관계) 순으로 분석해야 한다.(일반적으로 연구자가 꼭 원하는 내용이 아닌 경우 3변수를 넘는 상호작용은 분석하지 않는다.) carat(x)와 price(y) 두 변수를 선형 회귀 분석해보자면,
m1 <- lm(log(price)~log(carat), data=diamond) summary(m1)
$$log(price)=1.67×log(price)+8.46$$
$$price=e^{1.67×log(price)+8.46}$$
의 관계를 가짐을 알 수 있다.
잔차 분석을 해보면,
plot(fitted(m1), resid(m1)) abline(h = 0, lty=2)
잔차는 0을 중심으로 특이한 모양이나 경향을 보이지 않고 잘 퍼져있다.
잔차의 정규성을 보면,
shapiro.test(resid(m1))
왠지 정규분포 안 하는 느낌이 들기도 하는데,
qqPlot(resid(m1)) hist(resid(m1)) describe(resid(m1))
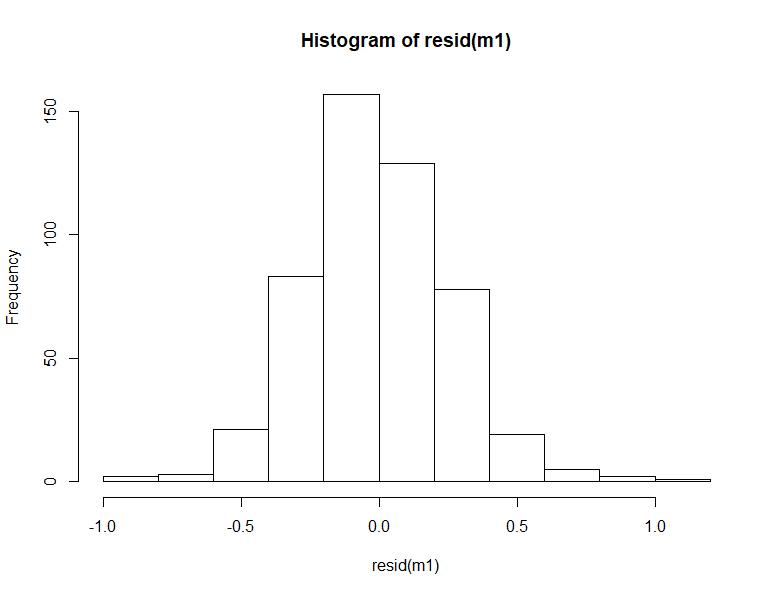

Q-Q plot이나 잔차의 histogram을 봐도 큰 문제없고 다만 분포가 위로 삐죽해서 (kurtosis 1.05) 그런 것이니 문제없이 넘어가도 될 듯하다.
두 변수의 관계를 그래프로 정리해보면
df <- data.frame(carat=seq(from=0.1, to=2, length.out = 100)) df$log_pred <- predict(m1, newdata = df) df$pred <- exp(df$log_pred) with(diamond, plot(carat, price, log = "xy")) with(df, lines(carat, pred, lty=2,lwd=1.5, col="red")) with(diamond, plot(carat, price)) with(df, lines(carat, pred, lty=2,lwd=1.5, col="red"))

3. category 변수화 한 후 분석
위와 같이 변환이 마법과도 같이 예쁜 형태를 지니게 해 주는 경우는 극히 드물다. 대부분 지저분한 형태를 지니기 때문에 4군이나 5군으로 나눈 후 ANOVA 분석하는 게 더욱 일반적인 모습이다.
quantile(diamond$carat, probs = c(0.25,0.5,0.75)) diamond$cate_carat <- cut(diamond$carat, breaks = c(0,0.4,0.7,1.02,Inf), right = T) summary(diamond$cate_carat) boxplot(log(diamond$price)~diamond$cate_carat) m2 <- aov(log(price)~cate_carat, data=diamond) summary(m2) TukeyHSD(m2)

우선 25%, 50%, 75% 지점을 찾아서 거길 기준으로 4군으로 나눈 후 (cut 명령어 내의 right=TRUE 명령어에 의해 (0, 0.4]와 같이 잘라준다. 이는 0 < x ≤ 0.4 를 의미한다. 기본 옵션은 right=FALSE), ANOVA 분석을 시행한 후 Tukey 방법을 통해 multiple comparisone을 시행한 결과이다. ANOVA분석을 한 이유는 Table 1에 필요하기 때문이다. 본 분석에는 선형 회귀 분석 결과를 쓰니 그것도 해보자.
m3 <- lm(log(price)~cate_carat, data=diamond) summary(m3)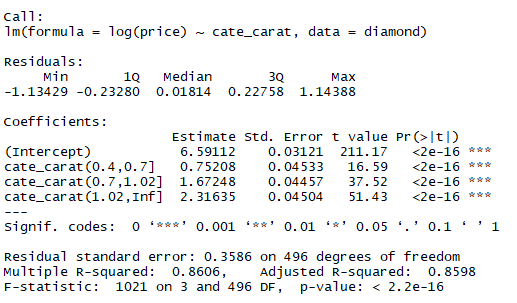
선형회귀 결과에서 Intercept 항목의 6.59는 carat 이 (0, 0.4]인 경우 price는 exp(6.59)=727.78$를 의미한다. (0.4, 0.7]의 0.75는 price가 exp(6.59+0.75)=1540.71$을 의미한다. 이렇게 4군으로 나누면 아무래도 통계적인 설명력은 감소할 수밖에 없다.
AIC(m1, m3)
AIC(Akaike information criterion)을 확인해보면, 선형 회귀의 결과가 더 낮은 AIC 수치를 보인다 (72.6 vs. 399.4). 위와 같은 결과라면 당연히 선형회귀 결과를 써야 하지만 앞에서도 언급했듯이 이렇게 예쁜 직선 형태를 보이는 경우는 그렇게 많지 않아서 차선책으로 4군이나 5군으로 나눈 후 분석을 한다. 군을 나눌 때 주의할 점은 무조건 예제에서 보여준 것처럼 quantile 기준으로 나누지 말고 임상적으로 의미를 가지는 절단점이 존재하면 그에 맞춰서 절단하는 것이 합리적이다. 그와 함께 고려해야 되는 점이 대상자가 너무 작은 군이 있으면 곤란하니 그것도 고려해야 한다는 점이다. 어찌 보면 앞의 내용과 상반되는 것일 수도 있지만 어차피 인생이 다 그런 거니 적당한 합의점을 찾는 것도 나쁘지 않을 것 같다.
4. 기울기가 다른 2개 이상의 직선으로 연결된 경우
여기부터는 약간 복잡한 내용이니 이해 안 가면 넘어가도 별 상관없다. 다만 이 이하 부분을 언급하는 이유는 이 세상 모든 관계가 직선은 아니라는 것을 보여주기 위해서 이다.
전기요금 같은 경우를 보면, 계절에 따라 다르고, 사용량에 따라 누진세가 붙는다. 또 사용자가 가정용이냐 사업용이냐에 따라 또 다르다. 나무 위키에 따르면 평균 가정의 전기사용량은 223KWh이고, 기본요금 (0~200KWh: 910원, 201~400KWh:1600원), 전력당 요금 (0~200KWh: 93.3원/KWh, 201~400KWh:187.9원/KWh)이 있다. 사실 요금체계는 더 복잡하지만... 뭐 전기세 계산을 위한 것도 아니고... 이 정도만 고려해보자.
set.seed(1234) df2 <- data.frame(x=rnorm(n = 100, mean = 223, sd = 60)) df2$y <- ifelse(df2$x>=200, 1600+200*93.3+(df2$x-200)*178.9, 910+df2$x*93.3) df2$y <- df2$y+rnorm(n = 100, mean = 0, sd = 1000) with(df2,plot(x,y))
(근데... 뭐라고 할까... 그냥 직선인 거 같은데? 원래 누진세가 이런가? 그냥 누진이고 뭐고 없고 쓰는 만큼 나오는 거였구나... 하여간 그래도 200 근처에서 꺾인 부분이 잘 보면 보인다.)
m4 <- lm(y~x, data=df2) summary(m4) residualPlot(m4)

이번에는 car package의 residualPlot 명령어를 이용해서 residual plot을 그려보았다. 예쁜 보조선을 그려주는데 보조선이 웃고 있다^^. 통상적으로 보조선이 웃고 있으면 2차 항을 투입해야 하지만 우리는 이미 2차항 의 곡선 모양이 아니라 2개의 꺾인 직선으로 이루어져 있음을 알고 있다.
df3 <- data.frame(t=seq(from=100, to = 300, length.out = 400),u=NA) for (i in 1:400){ df3$u[i] <- AIC(lm(y~pmin(x,df3$t[i])+pmax(x,df3$t[i]),data=df2)) } with(df3,plot(t,u,xlab="Hinge point",ylab="AIC value",type="l"))
위 그래프는 경첩 부위가 100~300 사이에 존재한다고 가정하고, 그 사이를 400 등분하여 그 개개의 경첩을 바탕으로 선형 회귀분석을 400회 시행한 결과이다. 대충 200 약간 전에 최소 AIC 수치를 가지는 부분이 보이는 것 같은데 더 자세히 보면,

경첩이 195에 존재할 때 최소 AIC 수치 (1676.7)를 보여 준다. 그럼 결과는
m5 <- lm(y~pmin(x,195)+pmax(x,195),data=df2) summary(m5) residualPlot(m5)

residual plot에서 웃는 모습이 사라졌다.
df4 <- data.frame(x=1:400) df4$pred4 <- predict(m4, newdata = df4) df4$pred5 <- predict(m5, newdata = df4) with(df2, plot(x,y, xlab = "Use (KWh)", ylab = "Electricity (Won)")) with(df4, lines(x,pred4, col="red", lty=2)) with(df4, lines(x,pred5, col="blue", lty=2))
처음 예상했던 것보다 누진세 비율이 좀 약하기는 했지만 어쨌든 선형 회귀에 비해서 경첩을 고려한 경우 더 잘 설명할 수 있었다. 근데 사실 이렇게 노가다를 할 이유는 없는게 earth package의 earth명령어를 쓰면 노가다 없이도 쉽게 된다. 물론 이번 경우도 category 변수화 하는 방법 사용 가능하다.
5. 비선형 관계
아예 비선형 관계를 보이는 경우도 존재한다.


첨부파일을 열어보면 L.minor dataset가 있다. 이 데이터는 substrate concentration에 따른 absorption rate를 나타내고 있다. 그리고 이는 Michaelis-Menten model을 따른다고 알려져 있다.
$$f(concentration, (K, Vm))=\frac{Vm×concentration}{K+concentration}$$
$$=\frac{1}{\frac{1}{Vm}+\frac{K}{Vm}×\frac{1}{x}}=\frac{1}{\beta_0+\beta_1\frac{1}{x}}$$
m6 <- glm(rate~I(1/conc),family = gaussian("inverse") ,data=L.minor) summary(m6) df5 <- data.frame(conc=1:200) df5$pred <-1/predict(m6, newdata = df5) with(L.minor,plot(conc,rate)) with(df5,lines(conc,pred,col="red",lty=2))

Michaelis-Menten model은 역수를 취할 경우 선형 회귀식으로 표현 가능해서 위와 같은 방식으로 진행했지만 nls 명령어를 이용해서 비선형 회귀 분석법으로 분석하는 방법도 있다.
여태까지 연속 변수와 연속 변수의 관계를 보기위한 여러가지 방법을 살펴보았다. 두 변수의 관계를 정의하는데에는 여러 방법이 존재하며 그 중 가장 납득 가능한 방법을 사용한다면 큰 무리 없이 분석을 진행할 수 있을 것이다.
6. Take Home Message
1) 두 연속변수의 관계가 무조건 직선이라고 생각하면 안 된다.
2) 기초 통계자료 및 그래프를 참조해서 적절히 변환하거나, 아니면 category 변수화 시키는 것이 가장 중요하다.
'R' 카테고리의 다른 글
로지스틱회귀분석 (R) (0) 2019.09.10 다변수분석법 (R) (0) 2019.09.07 탐색적 자료분석 3-3. 세 변수의 상호작용 (R) (0) 2019.08.28 탐색적 자료분석 3-2. 두 변수의 관계 파악 - 연속 변수 vs 범주형 변수 (R) (0) 2019.08.28 탐색적 자료분석 1. 정규성 검정 (R) (0) 2019.08.02